Teaching fractions is critical. Yet, students often struggle to master the concept of fractions. You can help these students by using the conceptual change process.
Mastery of fractions is one of the strongest predictors of success in high-school mathematics and helps in areas such as algebra. Therefore, it is vital that your students understand fractions.
Common Errors
Errors occur at the surface level. Common errors include:
When teaching fractions, many teachers have seen students make these sorts of common errors. And, many teachers correct their students by telling their students that they are wrong (or that a step is unnecessary) and repeating the correct way to do things.
There is nothing wrong with what these teachers have done. However, many errors are merely surface-level symptoms of an underlying misconception. Research shows that students struggle because they hold deeper misconceptions about fractions.
So, what should you do? Address their deeper misconceptions.
Using Conceptual Change to Address Misconceptions About Fractions
When students hold misconceptions, especially deep misconceptions, you should take advantage of the conceptual change process. Teaching fractions is an ideal time to use this process.

One frequent and deep misconception is rooted in students’ prior knowledge about whole numbers. It is known as whole number bias.
Prior knowledge can often make learning easier, but conceptually, the way whole numbers work is entirely different to the way fractions work. Here are some crucial differences.
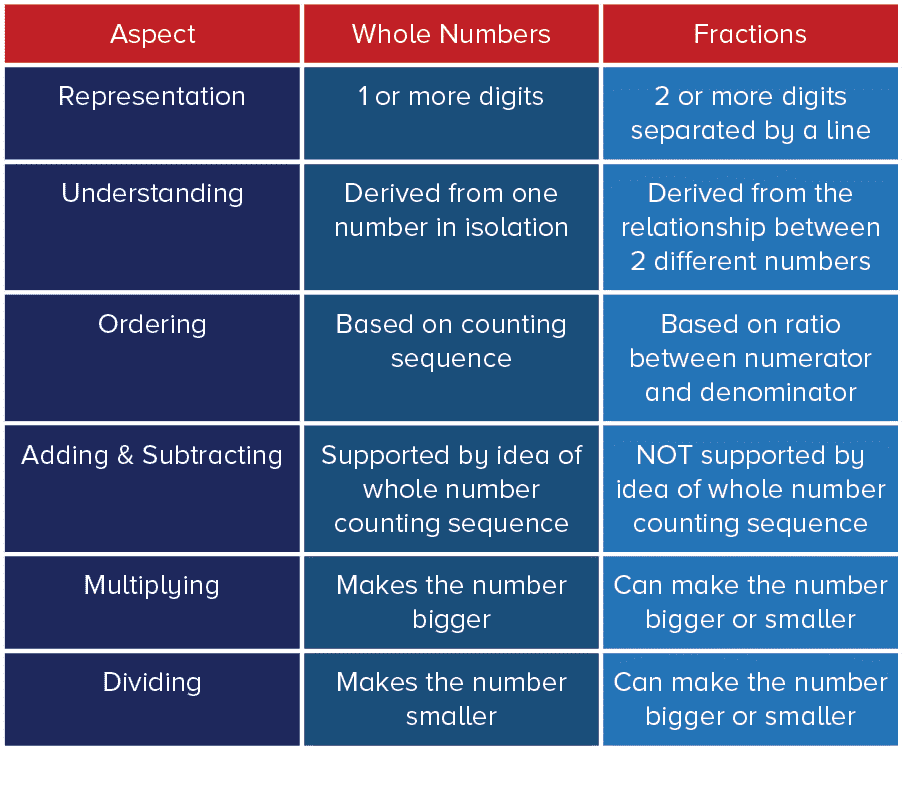
While many students represent fractions correctly, they mistakenly (and often subconsciously) use their understanding of whole numbers to try and understand fractions. It just doesn’t work!
For example, the whole number 8 means 8. It is bigger than 7 and smaller than 9. However, the value of 8 in a fraction depends on its relationship with the other number in the fraction. Consider these statements:

In these examples, you cannot figure out the value of 8 by its place in the whole number counting system. It is not that students’ understanding of whole numbers is wrong. Rather, the problem is they cannot make use of this prior understanding when working with fractions.
Numbers in fractions work in a totally different way. 8 can be bigger than 9, and smaller than 7. In a fraction, you cannot know what any number is worth (e.g. 8, 26, 3) without knowing the other number in the fraction.
With whole numbers, the number has a value in its own right. 8 is always 8. It is always less than 9 and more than 4. 28 is always 28, etc. In other words, you can understand the number in isolation.
With fractions, you can only understand each number in relation to the other number. More specifically, you can only understand fractions based on the ratio between the numerator and the denominator.
Many Students Don’t Get This
For most teachers and some students, this new understanding comes quite easily. However, for many students, it doesn’t.
Conceptual change is not likely to happen unless you clearly show the inadequacy of their existing beliefs. Therefore, when teaching fractions, you need to explicitly highlight the fact that:
Only after this has been done, should you start to teach your students about the fact that the value of a fraction (i.e. how big it is) comes from the relationship between 2 numbers – the numerator and the denominator.
When To Use Conceptual Change to Teach About Whole Number Bias
When should this be taught?
After looking closely at the Australian Curriculum, I believe it should be taught in Year 4.
In Year 4, students start:
However, if you teach older year levels, and your students struggle with fractions, it is worth going through this conceptual change process with them.
This is only one example of conceptual change with fractions. You can go through similar processes to dismiss other misconceptions, such as the notion that:
